来源:孤独症儿童教育研究中心 2024-01-31 10:00 发表于北京矩阵教学实施指南
“
矩阵教学(Matrix Training)是常用的帮助学生建立重组泛化的教学策略,不仅可以提升教学的效能,还可以培养发散思维,提升学生自发观察和自发学习的技能。但已有的研究中,矩阵教学的实施程序各不相同。今天小编结合发表在Behavior Analysis in Practice的文章《A Tutorial for Implementing Matrix Training in Practice》,梳理实施矩阵教学的步骤,为矩阵教学实践提供参考。
“
一、矩阵教学简介
矩阵教学使用矩阵作为规划教学的工具,把教学目标分解到矩阵的横轴和纵轴,将横轴与纵轴上的项目进行组合,在单元格中形成大量的教学内容。教师通过教学矩阵单元格中的部分内容,促使学生重组泛化出整个矩阵的内容。例如,教授学生“动作-对象”结构,如图1所示,可以将动作“摸”“扔”“推”放入纵轴,“球”“书”“车”放入横轴,教师教授学生学习“摸球”“扔书”“推车”三个组合,然后评估学生对矩阵中所有教学内容的掌握情况。
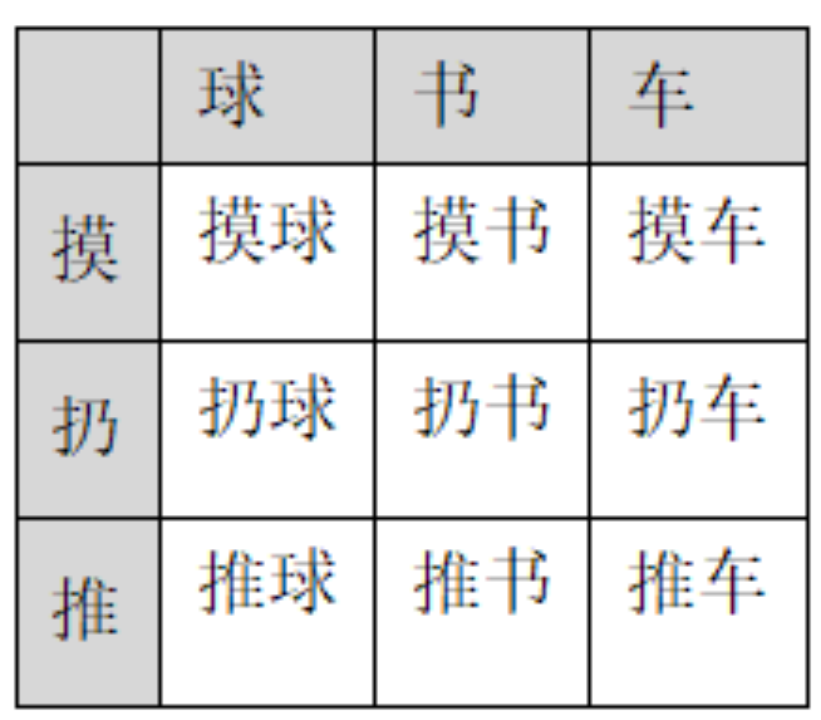
图1
我们来看矩阵教学所涉及到的一个概念:
重组泛化(Recombinative Generalization)是指学生能够把两个或更多已经习得的技能以不同的方式组合在一起,生成新的技能。例如,教授学生“红色的车”和“蓝色的球”后,学生学会重新组合“红色的球”和“蓝色的车”。
二、矩阵教学的发展
矩阵教学起源于Esper(1925)使用的微型语言系统(Miniature Linguistic System, MLS),微型语言系统即矩阵(一些研究中仍使用“微型语言系统”来代指“矩阵教学”),研究者认为,微型语言系统的有序性促成了衍生反应,但当时研究者并未探究产生衍生反应所需的教学条件。
在此基础上,一些研究得出了产生重组泛化所需的教学条件。Foss(1968)提出了矩阵教学的两种布局方式,分别是对角线教学(Diagonal Training)和逐步教学(Stepwise Training)。如图2所示,对角线教学是指教授对角线上的组合,在所教授的组合中,各维度上的项目仅出现一次,所以也称作非重叠教学(Non-overlap Training, NOV)。逐步教学是指除了对角线上的组合,还需要再教授一组包含各维度中所有项目的组合,所以也叫重叠教学(Overlap Training, OV)。教学完成后,评估未经教学的组合是否产生了重组泛化。
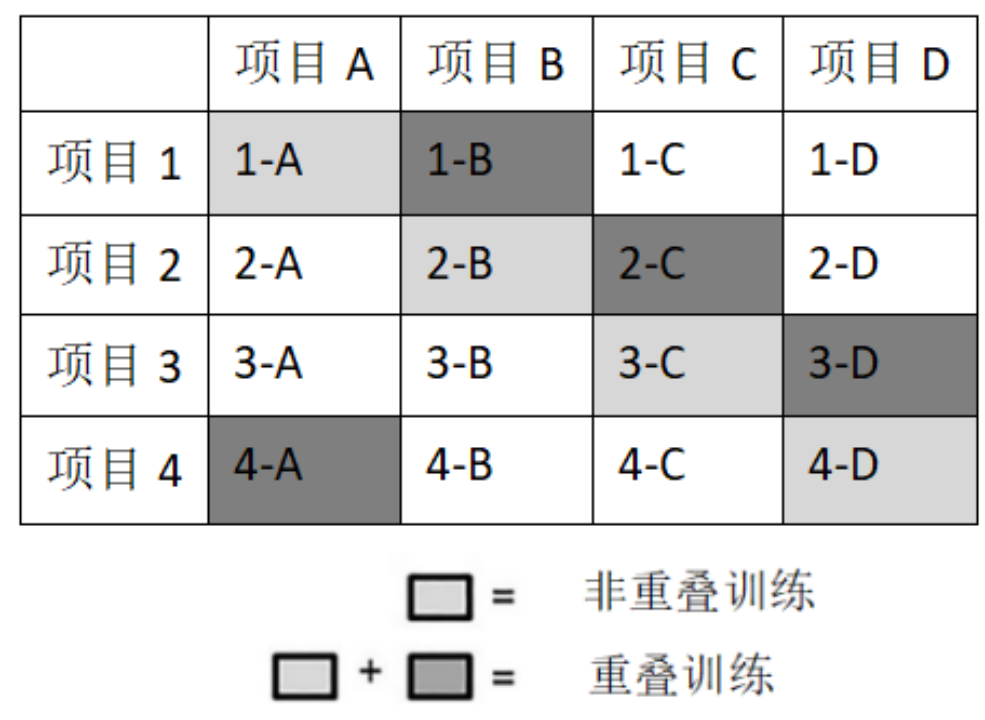
图2
随后,矩阵教学的应用范围逐步扩展至发展障碍学生生成性技能的教学。由于孤独症学生存在思维刻板、认知灵活性不足等特点,较难产生生成性技能,矩阵教学在孤独症学生教学中有着广泛的应用。
三、矩阵教学实施指南
矩阵教学可以广泛应用于不同的教学领域中,教学中使用矩阵的目的有二:
一是所教授的技能是一种行为模式,未来需要重组泛化到更多内容上,因此需要矩阵教学建立重组泛化能力。例如,教授学生命名“过滤勺在盒子上边”,需要学生未来能够使用介词命名更多物品的位置,如“糖在抽屉里边”。
二是需要教授的内容很多,需要使用矩阵来规划教学,以便只教授其中一部分就能促使学生掌握所有内容,提高教学效率。这两种情况下,教师可以使用矩阵教学。以下为矩阵教学的实施步骤。
(一)确定矩阵教学的目标和内容
根据学生的发展需求和自身水平,选择适合学生的教学目标。例如,《培智学校义务教育课程标准(2016版)》中生活语文的学段目标包括“观察校园环境,能用自己的方式说出观察所得”,教师可以用矩阵教授“(谁)在(做什么)”的句式,根据学生的语言能力,具体方式可以选择说、写或用辅助沟通系统表达。
在确定教学目标时,要注意教学目标必须能分成至少两个维度,每个维度都由独立的刺激控制。
图1-1是一个正确的例子,“识读钟表上的时间”任务可以分成两个维度,时针刺激控制小时反应,分针刺激控制分钟反应。
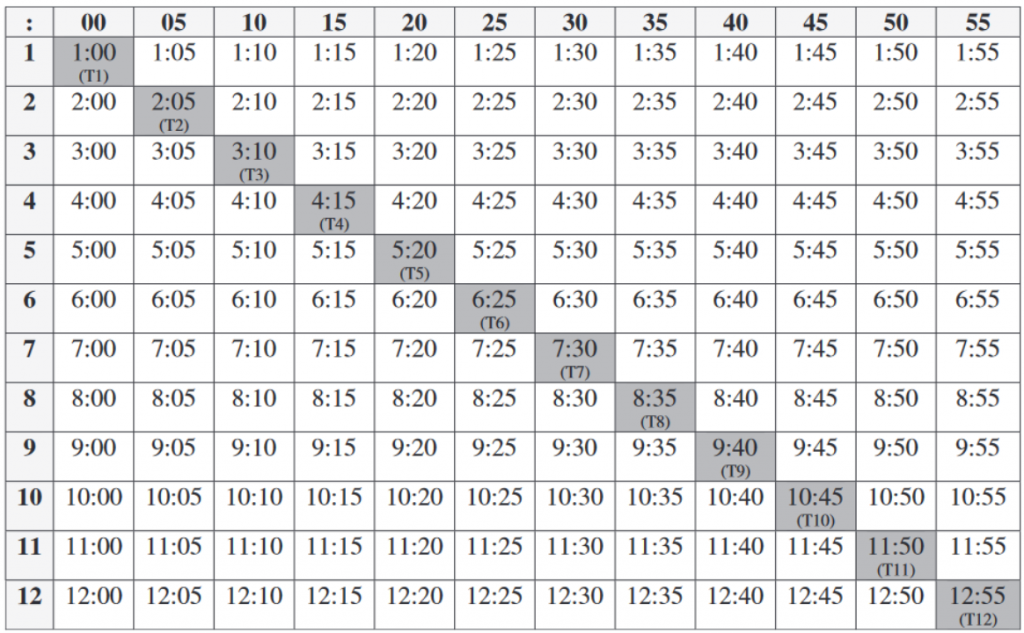
图1-1
再举一个错误的例子,“酒店”是一个刺激控制下的整体,不是由“酒”和“店”独立控制的两个反应,此类目标不能使用矩阵进行教学。
(二)设计教学矩阵
确定教学目标后,教师需要将教学目标分解为两个或更多维度,选择每个维度上的项目,组建矩阵。例如,将“命名位置”分解为“物品”维度和“方位介词”维度,选择4种物品放入横轴,选择4种方位介词放入横轴,用行列交叉形成的组合填充矩阵,如图2-1。
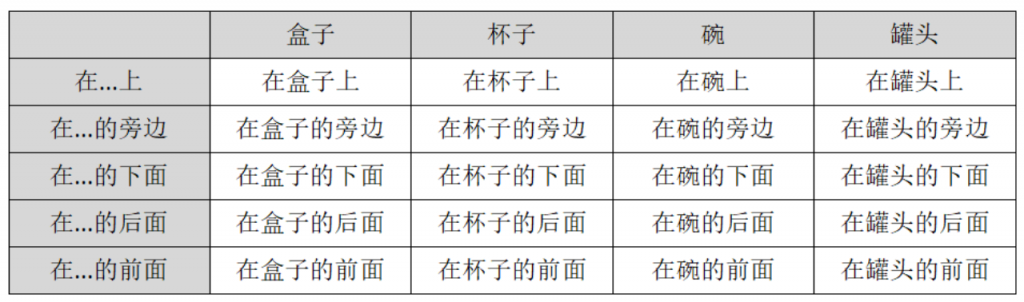
图2-1
选择项目时需要注意两点:
一是选择每个维度上的项目时要注意使矩阵中不同维度的项目之间可以任意组合,产生的所有组合都有意义。
图2-1是一个正确的例子,纵轴是方位介词,横轴是物品,不同维度的项目可以任意组合。
图2-2是一个错误的例子,“拿墙”或“扔墙”是无意义的组合,“扔订书机”是危险的行为,不宜放入矩阵进行教学。
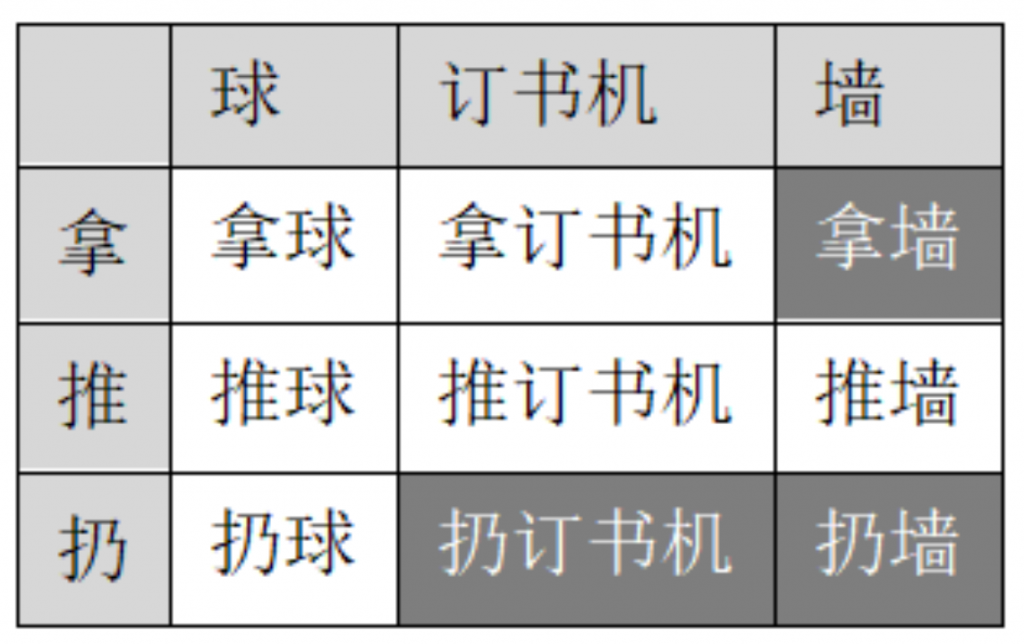
图2-2
二是同一维度的项目在组合中须起到相同作用。
图2-3是一个正确的例子,纵轴是颜色,横轴是颜色所描述的物体,同一维度的项目发挥的作用相同。
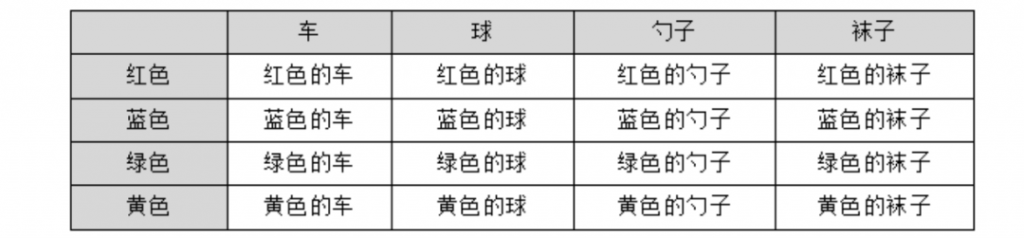
图2-3
再举一个错误的例子,汉语拼音中,“j-”和“n-”与“-u”组合时,“ju”和“nu”中“-u”的发音不同,因此不宜放入矩阵中进行教学。
考虑到教学效率,如果学生已经掌握了技能中的某一部分(如“主-谓-宾”中的“主-谓”部分),那么在矩阵教学中就不再将其分开,而是整体作为矩阵教学的一个维度,形成一个更简洁的矩阵。
具体整合方法如图2-4、2-5所示:图2-4是一个包含主语、谓语和宾语的三维矩阵,如果要将主语和谓语整合到一个维度,则须在包含主语和谓语两个维度的平面中提取对角线,该对角线上的组合放入二维矩阵的纵轴,宾语放入二维矩阵的横轴,就可以形成图2-5所示的矩阵。
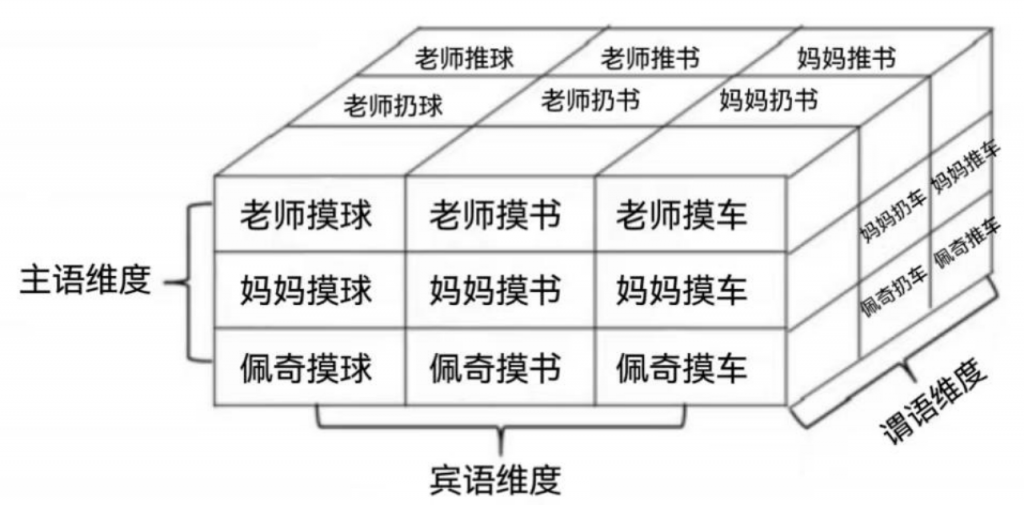
图2-4
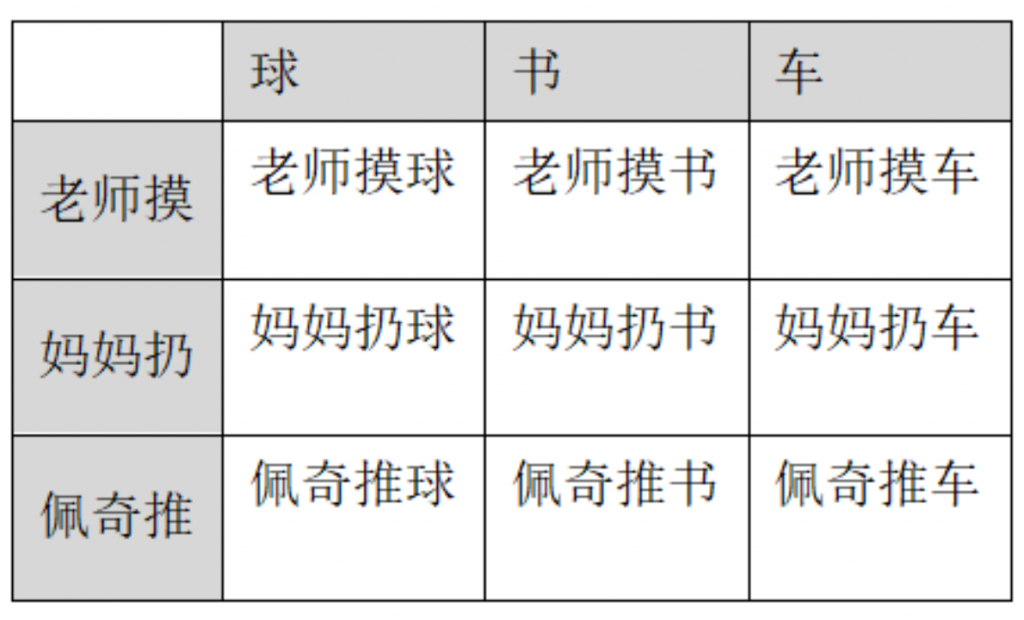
图2-5
(三)进行矩阵教学
完成矩阵的设计后,教师需要选择布局方式,确定教学顺序,准备教学材料,然后开展矩阵教学。以Frampton等(2016)为例,向大家介绍上述过程,其中使用的矩阵如图3-1所示。
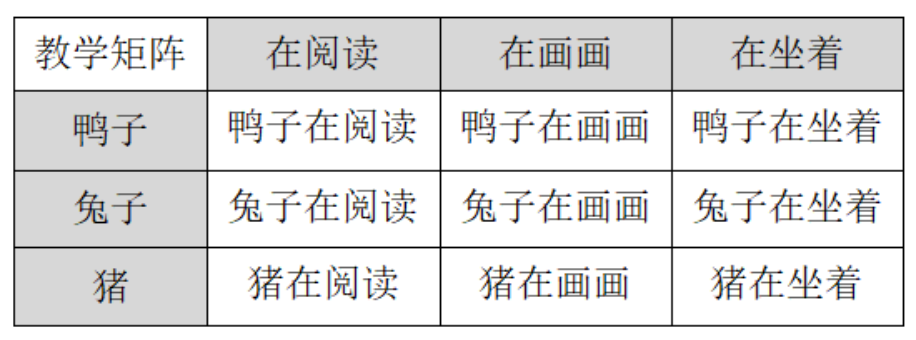
图3-1
教师要教授学生“角色-动作”组合,选择学生能够命名的“角色”和“动作”放入纵轴和横轴。由于两个维度上的项目都是学生已掌握的,因此教师选择非重叠教学的布局方式,教授教学矩阵中对角线上的3个组合,对3个组合同时进行教学。每个教学时段包含9个回合,9个回合中,3个组合各教授3次。
矩阵教学是一种教学规划策略,经常与其他循证教学方法结合使用,教师需要根据诸多因素灵活决定教学程序,满足学生独特的教学需求,下面分别列出了三个方面的决策参考。
1. 选择布局方式
Frampton等(2016)的教学实例中,由于两个维度上的项目都是学生已掌握的,所以教师选择非重叠教学的布局方式。但如果矩阵中包含学生未掌握的项目,可能需要采用重叠教学的布局方式。例如,Curiel和Curiel(2021)教授学生计算纸币和硬币的总金额,学生此前不熟悉硬币和纸币,所以选用重叠教学的布局,教授图3-2中深色的6种组合。
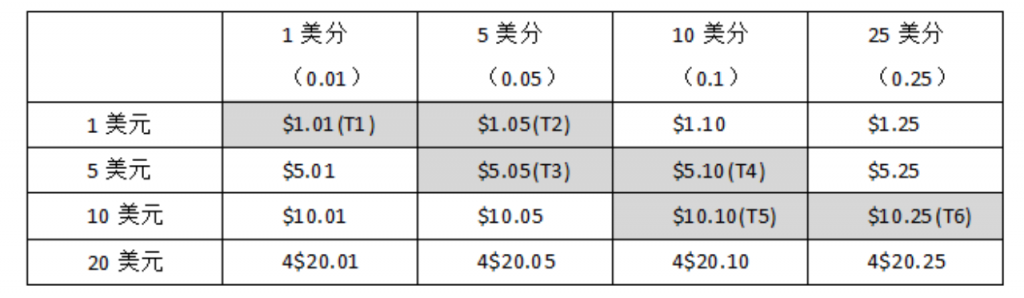
图3-2
2.确定教学顺序
Frampton等(2016)的教学实例中,由于矩阵较小,所以教师同时教学对角线上的3个组合。但矩阵较大时,教师则要按照一定顺序进行教学,可以将需要教学的组合分组,依次对每组进行教学。例如(图3-3),Curiel和Curiel(2021)的教学实例中,共需教授6个组合,分3组进行,第一、二阶段教授T1和T2,第三阶段教授T3和T4,第四阶段混合教授T1-T4,第五阶段是T5和T6,第六阶段混合教授T1-T6。另外,也可以将矩阵划分为几个子矩阵,如图3-3所示,子矩阵Ⅰ的教学及探测完成后,再进行子矩阵Ⅱ的教学及探测,以此类推完成子矩阵Ⅲ和Ⅳ的教学及探测。
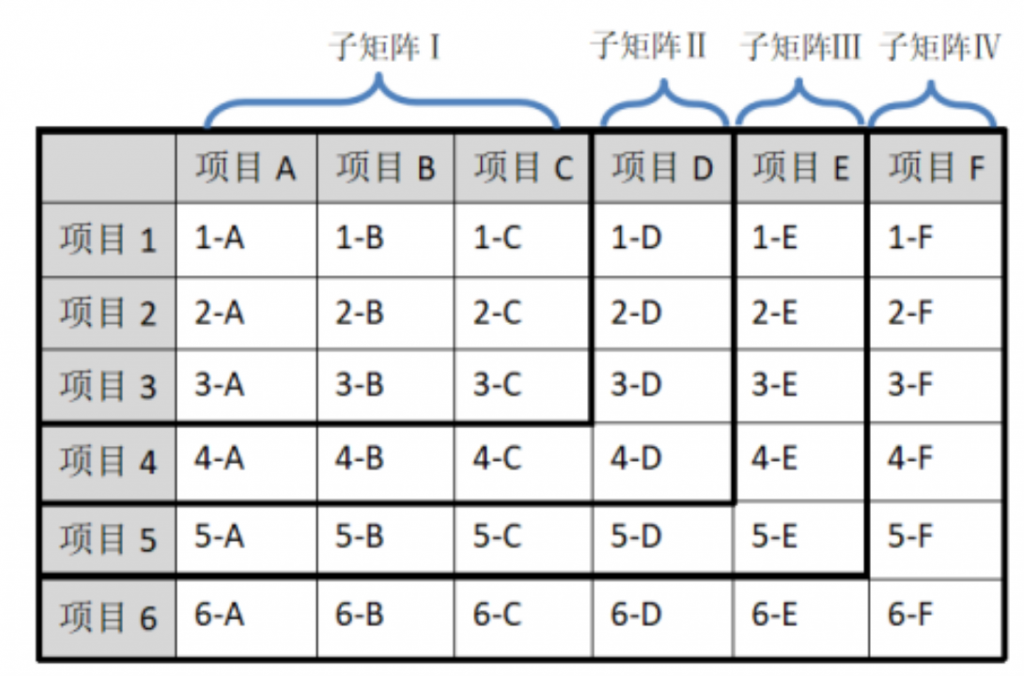
图3-3
3. 准备教学材料
Frampton等(2016)的教学实例中,教师使用动物模型做出相应动作,因此只准备3种动物模型即可,相比于制作每个“角色-动作”组合的图片或视频,十分灵活高效。由于矩阵可以产生大量的教学内容,教学材料的准备可能十分费时费力。有时,同一教学过程可以使用不同教学材料来实现,此时教师应注意选择使用灵活高效的教学材料。
(四)评估教学效果
矩阵教学过程中,教师要及时评估重组泛化的情况。为了提高评估效率,可以在每个时段评估时随机选择未经教学的组合进行探测。例如(图4-1),在每个时段中同时教授1-A、2-B和3-C三个组合,可以在时段1中探测组合1-B、2-C和3-A,在时段2中探测组合2-A、3-B。
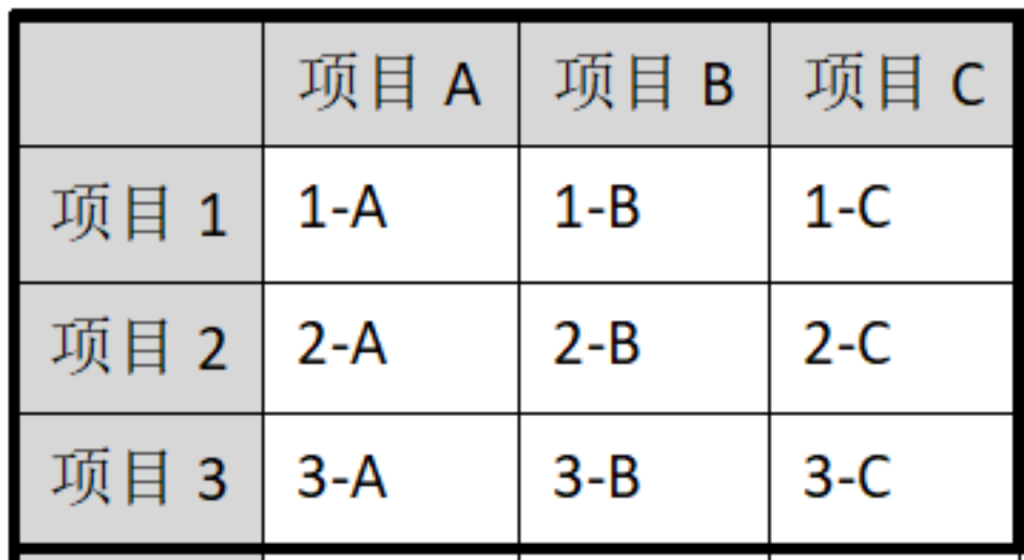
图4-1
所有教学完成后,教师要对教学效果进行完整的评估。以Frampton等(2016)中的后测为例向大家介绍评估流程,其中使用的矩阵如图4-2所示。教师先依次探测教学矩阵中的所有组合,评估矩阵内泛化效果,再依次探测泛化矩阵中的所有组合,评估矩阵间泛化效果,两个矩阵的探测程序一致。但如果泛化矩阵中存在学生未掌握的项目,需要在评估前进行教学。以“鸭子在阅读为例”的一个探测回合为例,教师用动物模型做出相应动作,问学生:“发生了什么?”给学生5s时间做出反应,对学生做出的正确或错误的反应,教师均给予中性反馈,如“好的”。一个时段的探测包含9个回合,完成5个回合的探测后,教师穿插一个学生精熟的任务,强化学生的正确反应,一共探测3个时段。由于在后测中评估的大多数反应未经直接训练的,且探测在没有强化的条件下进行,因此学生反应相对不稳定,后测的掌握标准相比于教学阶段略有降低,为连续3个探测时段的正确率不低于78 %,低于该标准则需要进行补救教学。
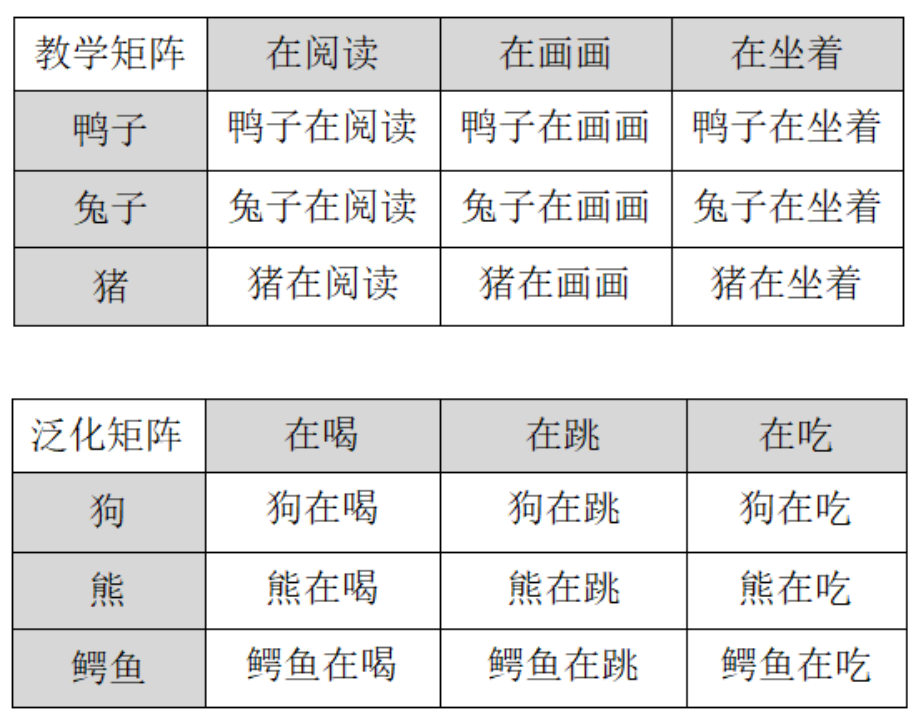
图4-2
除矩阵内泛化和矩阵间泛化外,矩阵教学还可能泛化到不同人员、环境和技能上。例如,评估在教室中的习得的技能,泛化到日常生活中的情况。
完成评估后,教师需要对评估结果进行分析,以指导进一步的教学。以下为可能出现的结果和补救建议(图4-3):
1. 如果教学矩阵中所有组合均不达标,则可进行重复教学,以加强教学效果;或修改评估程序,如加入适当的动机操作。
2. 如果教学矩阵只有未经教学的组合不达标,则可对非对角线组合进行补充教学。
3. 如果泛化矩阵中的组合不达标,则可对泛化矩阵进行补充教学。
4. 如果所有矩阵均达标,则可扩展矩阵或设计新矩阵进行教学和评估,或继续评估其他泛化效果。
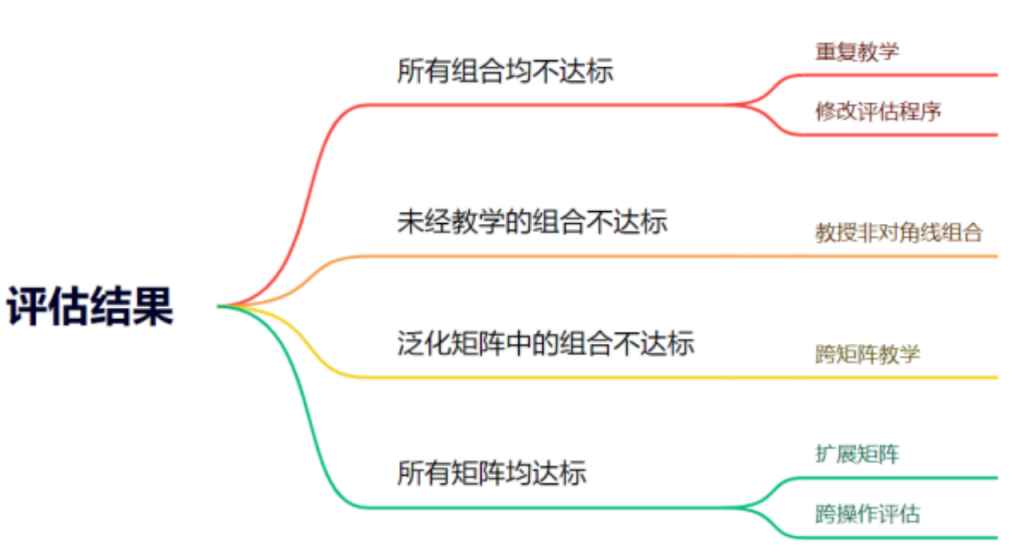
图4-3
参考文献:
[1] Frampton, S.E., Axe, J.B. A Tutorial for Implementing Matrix Training in Practice. Behav Analysis Practice 16, 334–345 (2023). https://doi.org/10.1007/s40617-022-00733-5
[2] Curiel ESL, Curiel H, Li A. Generative time telling in adults with disabilities: A matrix training approach. Behavioral Interventions. 2020; 35: 295–305. https://doi.org/10.1002/bin.1714
[3] Curiel, E.S.L. and Curiel, H. (2021), Teaching receptive money identification skills using matrix training: A preliminary investigation. Behavioral Interventions, 36: 572-582. https://doi.org/10.1002/bin.1794
[4] Frampton, S.E., Wymer, S.C., Hansen, B. and Shillingsburg, M.A. (2016), The use of matrix training to promote generative language with children with autism. Jnl of Applied Behav Analysis, 49: 869-883. https://doi.org/10.1002/jaba.340
[5] Suchowierska, M. (2006), Recombinative generalization: Some theoretical and practical remarks. International Journal of Psychology, 41: 514-522. https://doi.org/10.1080/00207590500492534
[6] 胡晓毅,程霞.孤独症儿童概念教学策略述评[J].中国特殊教育,2019(01):25-32+40.
[7] 刘佃振,陈建军,宿淑华,.矩阵训练应用于孤独症儿童言语行为的干预研究述评[J].中国特殊教育,2022,(10):54-62.
编辑:陈欣雨
审核:王印
